这里我再挂一道最近新编的平面几何题，适合于初二同学。供大家思考，到公开课时从正确解答者中抽奖。当然对奖品的期望可不能过高：） 一切还是以兴趣为重。

[ 本帖最后由 老封 于 2010-3-10 13:35 编辑 ].

已知：有两个直角三角形，其一两直角边长分别为a，b（a＞b）；另一两直角边长分别为a＋b，a－b。∠1和∠2分别是这两个直角三角形中较小的内角。
求证：∠1＋∠2 ＝ 45°。.

请有兴趣参加征解的初二同学（其它年级也可）将解答过程或解题思路写在自备纸上，公开课那天带来即可。.

tg(∠1+∠2)＝（tg∠1+tg∠2)/(1-tg∠1tg∠2)

=(b/a+(a-b)/(a+b))/(1-(b/a)*((a-b)/(a+b)))=1

tg∠1=b/a

tg∠2=(a-b)/(a+b)

tg(∠1+∠2）＝1

∠1＋∠2＝45°



[ 本帖最后由 炫炫爸 于 2007-3-2 16:08 编辑 ].

引用:

原帖由 炫炫爸 于 2007-3-2 13:17 发表
tan(∠1+∠2)＝（tan∠1+tan∠2)/(1-tan∠1tan∠2)

=(b/a+(a-b)/(a+b))/(1-(b/a)*((a-b)/(a+b)))=1

tan∠1=b/a

tan∠2=(a-b)/(a+b)

tan(∠1+∠2）＝1

∠1＋∠2＝45°

  

果然身手不凡！
你是动用了秘密武器，呵呵.

tan是什么?看不懂.

看到了吧,开始搞破坏了
炫炫爸 就是F4之一,厉害吧.

引用:

原帖由 都都妈 于 2007-3-2 13:25 发表
看到了吧,开始搞破坏了
炫炫爸 就是F4之一,厉害吧

没关系的，
他的思路似乎还不会影响到初二同学的革命干劲。
加油干吧！会有绝顶精彩的方法。.

老封是要大家用几何方法，我这个只能算一题多解。

[ 本帖最后由 炫炫爸 于 2007-3-2 16:13 编辑 ].

厉害.

这是几何，还是解三角。
都还给老师了.

Excel告诉我: tan(number)是"返回给定角度的正切值".
我们在中学里学过这个吗?没印象..

这题会有简便方法的。
解答中尽量不要用到高级的工具和概念。.

引用:

原帖由 都都妈 于 2007-3-2 13:23 发表
tan是什么?看不懂

tan是计算机语言里的写法，数学上是tg，我改了。.

老封，不要急，才半天，我担心你就挂出解题方法了。.

引用:

原帖由 炫炫爸 于 2007-3-2 16:11 发表


tan是计算机语言里的写法，数学上是tg，我改了。

不用改，现在新的课本已统一为tan了。.

遵照老封的建议，将解法隐藏。

不过，老封你也应将“引用”隐藏啊！

[ 本帖最后由 春笋逢春雨 于 2007-3-2 16:33 编辑 ].

恭喜了。建议您尽早将此帖暂且隐藏，天机不可泄漏！

[ 本帖最后由 老封 于 2007-3-2 16:38 编辑 ].

解法已隐藏，引用也应隐藏啊。.

引用:

原帖由 春笋逢春雨 于 2007-3-2 16:36 发表
解法已隐藏，引用也应隐藏啊。

呵呵.

全还老师了 老封老师收大点老点的脑子已经不灵的学生吗?.

不敢当。不过几何是所有人都可以去学的有趣学问，我们对美的追求应该都是共同的！.

是的,还好记得黄金分割点,好象是0.618.

引用:

原帖由 老封 于 2007-3-2 16:17 发表

不用改，现在新的课本已统一为tan了。

看来我是东西没有还给老师，只是没有及时了解最新行情。.

引用:

原帖由 都都妈 于 2007-3-2 16:50 发表
是的,还好记得黄金分割点,好象是0.618

那个都妈你是不会忘的，因为你当初选男朋友就是按上身和下身黄金分割选的。 .

建议封老师将公布答案的时间设置为2天， ！.

这个你怎么知道的?还真是.你是苏联的KKB吧.

报告封老师，我几何法也有了。

另外我还用坐标法做了。 .

他自己有切身体会,所以特别理解都都爸.

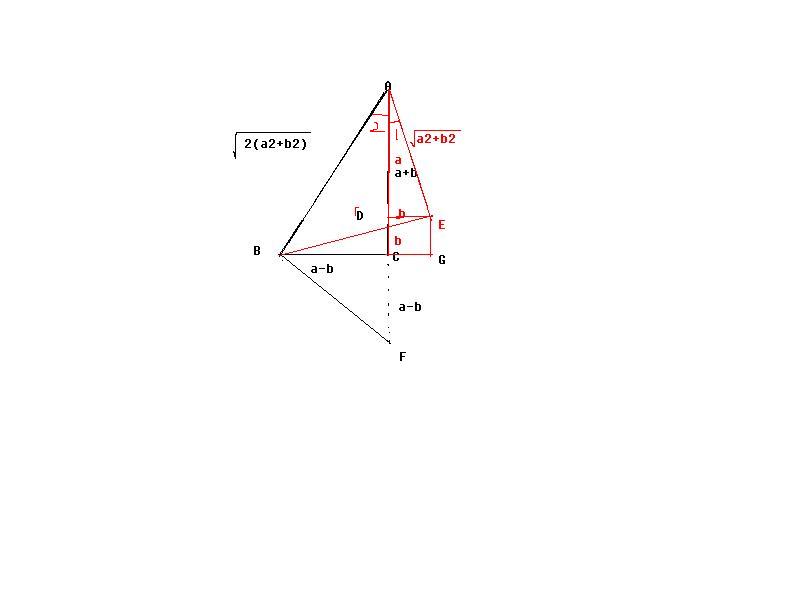
延长AC至F点，使CF=BC=a-b
AF=(a+b)+(a-b)=2a
取AF中点D，则DC=b,AD=a
延长BC至G,使CG=CD=b,从D点作CG的平行线DE,并使DE=b，则DEGC为边长=b的正方形，连AE
在三角形ADE中，AD=a,DE=b，且角ADE是直角，则角DAE为图1中的角，且AE=a^2+b^2(开根）
连BE，在三角形BEG中，BG=(a-b)+b=a,EG=b，则BE=a^2+b^2(开根）
在三角形ABC中，AB^2=AC^2+BC^2=(a+b)^2+(a-b)^2,所以AB=2（a^2+b^2) (开根）

所以在三角形ABE中，由于AE^2+BE^2=AB^2,且AE=BE
所以可以得出角BAE=45
角BAE=角BAC+角EAC
也就得出两个角的和=45

炫炫爸的方法最好了，如果学过tan的公式，首选炫炫爸的方法。

[ 本帖最后由 daifangsandy 于 2007-3-2 18:05 编辑 ].

引用:

原帖由 老封 于 2007-3-2 12:16 发表
这里我再挂一道最近新编的平面几何题，适合于初二同学。供大家思考，到公开课时从正确解答者中抽奖。当然对奖品的期望可不能过高：） 一切还是以兴趣为重。

我倒，题目太难了，想破脑袋也想不出，强烈要求冯先生（啊，什么时候封先生成黑社会头目了，浪本浪流……）收我为徒弟，我学费加倍奉上。.

夜饭漆好了，丁丁星星做题目，港老石咸画，题目并8奶的，8过妹有米道格。

进糟夜饭漆对下，高蛋白，到底游泳场，漆了6只对下，响彻来6中板法，铁上来2中， 娘冯先生过木，阿拉8大有文化的，错别子妹多格，8号一丝。

[ 本帖最后由 老姜 于 2007-3-2 20:12 编辑 ].

奖没了！.

引用:

原帖由 上海的考拉 于 2007-3-2 19:24 发表
奖没了！

我用骗来的奖金交学费，哥哥姐姐叔叔阿姨大嘎苦里我，我一接动，又开水写错别子了。.

引用:

原帖由 炫炫爸 于 2007-3-2 13:17 发表
tg(∠1+∠2)＝（tg∠1+tg∠2)/(1-tg∠1tg∠2)

=(b/a+(a-b)/(a+b))/(1-(b/a)*((a-b)/(a+b)))=1

tg∠1=b/a

tg∠2=(a-b)/(a+b)

tg(∠1+∠2）＝1

∠1＋∠2＝45°

  

炫炫爸像黑社会的打手，打相打不讲规矩的，打法打法，眼看自己要吃亏了，就撒一把石灰，别人眼睛看8见了，炫炫爸一用力，就把敌人推到黄浦江里“氽馄饨”了。

初二学生8好用两角和的正切公式的，一定要用3角，74用余弦定理也4可以的。.

初二参加高中全国数学竞赛的都有。.

看得偶昏头六冲,七荤八素. 学习,学习,再学习!.

平面上有11条直线互不平行，试说明，在所有的交角中，至少有一个角小于17度。.

上海滩结束了，再跑上来看看，奖金是不是开始发放了。生活中的封先生，比电视里的冯先生要可爱多了。

炫爸爸的题目好像满简单的，用反证法：

将所有直线平移到过同一点，就相当于得到22条射线，若每相邻两条射线所夹的角均>=17度，则周角>=17*22=374度，矛盾了。.

要从头补起来了
以后孩子真要学起几何来，问我，我可是一问三不知啊。汗哒哒滴，哒哒滴，哒哒滴…….

偶电脑技术实在太差了，根号2愣是不会写，所有画图都是 word上拼的，最后还得图片形式上来
十多年没接触几何了.

虽然知道tan是什么意思，但是证明除两个角相加等于45度有意义吗？对大多数人来说还是没有意义的。.

引用:

原帖由 kecy 于 2007-3-3 10:29 发表
偶电脑技术实在太差了，根号2愣是不会写，所有画图都是 word上拼的，最后还得图片形式上来
十多年没接触几何了

方法不错。.

这个方法稀饭的.

一张长方形ABCD的纸片，把C角顶点折到AD边上，包括A点和D点，问C点在AD边什么位置时，其折痕最短，在什么位置时，其折痕最长。

[ 本帖最后由 炫炫爸 于 2007-3-5 12:00 编辑 ].

引用:

原帖由 炫炫爸 于 2007-3-5 11:58 发表
一张长方形ABCD的纸片，把C角顶点折到AD边上，包括A点和D点，问C点在AD边什么位置时，其折痕最短，在什么位置时，其折痕最长。

为避免混淆，我们把线段AD上的C叫做C1，原来的C还是叫做C，又称折痕为线段EF（E，F分别在线段AB，CD上）。

显然，直线EF为线段CC1中垂线，则容易证明：EF=CC1（利用全等三角形）。当C1与A重合，CC1最长，EF也最长；当C1与D重合，CC1最短，EF也最短。.

接棍额.

折了一下，感觉不大对，AB>AD和AB<AD也一样吗？我试试。.

这两天有事没能上网，今天一看大出意料。
没想到我公布的这个题引起了大家热烈的讨论,而且真的涌现出不少漂亮的证法，真是高手如云啊！
不过我要补充一下，这题最早的正确解答是由 春笋逢春雨 于 2007-3-2 16:18 发表的：

将二个直角三角形画在一个  长为a+b  宽为a  的长方形内，然后添加辅助线，得到一个边长为b的直角等腰三角形，一个边长为a的正方形，一个直角边分别为根号2a、根号2b的直角三角形，这样就可证出角1加角2等于45度了。

我打算再编一个新题，来替代这个已被大家解秘的题，作为公开征解。不过还得过两天才发表，到了周日公开课时，我希望看到像这题一样的热烈的局面。

不过这个新题的难度该如何把握呢？应该也不能太难吧，因为要适合初二的小同学们。所以我正在绞尽脑汁呢。

让大家拭目以待吧！.

引用:

原帖由 炫炫爸 于 2007-3-5 13:32 发表
折了一下，感觉不大对，AB>AD和AB<AD也一样吗？我试试。

hehe，中午看得匆忙，要吃饭了，看成正方形了。.