1.同底数幂的除法
见34楼 “8. 同底数幂的乘法、同底数幂的除法”
同底数幂相除,底数不变,指数相减。

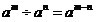
(m、n都是正整数,且m>n, a≠0)
任何不等于零的数的零次幂为1,

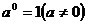
2.单÷单
①法则:系数、同底数幂、字母指数
②注意点:先确定符号,再计算系数,再用法则;对于只在被除式里含有的字母,连同其指数作为商的一个因式,避免遗漏;系数是分数的计算。
提高运算结果的正确率。
3. 多÷单
①法则:“每一项”
②注意点:不要跳步,不要漏项,不要出现符号错误等等;特别地法则不要用错。
说明:
(l)多项式除以单项式,商式与被除式的项数相同,不可丢项;
(2)能说得出式子每步变形的依据;
(3)要养成检验的习惯,利用乘除逆运算,检验除的对不对。
总的来说,在之前学了整式的乘法后这里学除法没有太大的问题。
4.练习.