接上文:
4) & 5) 瞄准和射击。
所谓瞄准和射击过程,就是你一个一个地尝试上述武器来攻克目标。
你需要构造出与你的所选知识点(武器)类似的图形(必要时添加辅助线),然后使用各种几何推理方法(全等与相似形、旋转、平移、翻折等)推导出你所构造的图形符合你的所选知识点的几何性质,于是命题得证。
拿具体例子来看。
证法1和2: 所选的知识点(武器)是“等腰三角形底边的中垂线”性质。
那我们必然要把待证明的两个线段放到一个等腰三角形中去看吧?那如何构造这个等腰三角形呢?
最关键点在于,这两个线段必定是:一个线段在该等腰三角形的底边上,另外一个线段就在此底边上的中线上。而且两个线段的交点必是底边的中点。 所以构造此等腰三角形的要诀就在刚才这句话中:
两个线段的交点必是底边的中点。那么如下图,想构造的等腰三角形只有两种可能,
情形1) 线段1作为此三角形的底边的一半,线段2则是底边上的中线。
情形2) 或反过来,线段2作为此三角形的底边的一半,线段1则是底边上的中线。

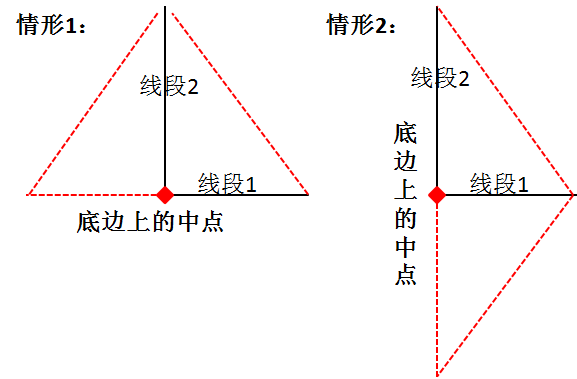
根据此要诀我们马上自然地得到了证法1 和 证法2的辅助线画法:
证法1:构造的目标等腰三角形是 DPB, BE在地边上,DE是中线。
证法2:构造的目标等腰三角形是 DBS, DE在地边上,BE是中线。
于是问题转化成为:
证法1:要证明 DPB 等腰三角形是(DE则是中垂线), 亦或 DP=DB
证法2:要证明 DBS 等腰三角形是(BE则是中垂线), 亦或 BD=BS
到这里,问题就相对简单了:
看看已知条件中啦些还没用到:E除了是证法1的PB的中点,或证法2的SD的中点外,还是线段AF的中点。
看到这个要马上想到武器库中的知识点:两个线段相交且互相平分,则他们构成了平行四边形的对角线。
所以证法1的PABF是矩形, 故PDCF也是矩形, 所以 AP=CF=CA=DB(反复运用矩形的对角线相等即可),所以 DPB果真是等腰三角形。
同理,证法2的ADFS是平行四边形,FS//AD, 故FS与FC共线, 所以 BS=BF+FS=BF+DA=BF+CB=CF=AC=DB(反复运用平行四边形的对边相等和对角线相等即可),所以 DBS果真是等腰三角形。
上述思路整理即可得到证明过程。
有人可能会问: 有关中点的题型中不是有这么个套路么:从中点处延长相关线段1倍。像上述的证法1, 2你分析半天,最后还不都是符合这个套路么? (证法1 在中点E处延长BE, 证法2在中点E处延长DE)
问得好,这道题是不用费这个劲分析,直接按套路就可以不问青红皂白地画出证法1 或 证法2的辅助线。考试时我也建议碰到有类似套路不妨马上去尝试下,毕竟时间有限,说不定套路可以帮你速战速决,但:
1) 平时我建议还是多使用分析与综合的思维来提升技巧。平时只管套路少动脑筋的话水平提高得慢。
2) 套路不是总奏效,千万别吊死在套路上了。比如下面这道题是用“逢中点就倍延”的方法恐怕只是死胡同吧,虽然满眼看到的条件都是中点、中点的:
比如下图中,ABCD是正方形,E是AB上的中点,F是BC边上的中点,CE与DF相交于点G。求证: 三角形AGD是等腰三角形。


这道题目用“逢中点就倍延”的老套路就不太奏效了.
所以考试时碰到套路无效时,千万别被套路把思维给堵死了,赶紧开动脑筋另辟蹊径。
[
本帖最后由 高山仰止 于 2013-11-26 16:23 编辑 ].