1. 有必要再提的一个公式
(x+a)(x+b)=x^2+(a+b)x+ab
反过来, x^2+(a+b)x+ab=(x+a)(x+b)
2.二次三项式
多项式ax^2+bx+c (a≠0)称为关于 x的二次三项式,其中ax^2 称为二次项,bx为一次项,c为常数项.
3.十字相乘法
①依据(算理):
对于二次三项式x^2+px+q,如果能够把常数项q分解成两个因数a、b的积,并且a+b等于一次项的系数p,那么它就可以分解因式。
即x^2+px+q= x^2+(a+b)x+ab=(x+a)(x+b)
②表示:可以用十字交叉线表示

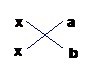
③十字相乘法分解因式的步骤:
(1)把常数项分解因数;(2)尝试十字图,使经过十字交叉线相乘后所得的积的和为一次项系数;(3)写出因式分解的结果。
④技巧:
对二次三项式x^2+px+q进行因式分解,它的方法是“拆常数项,凑一次项”。
⑤符号规律:
当q>0时,a、b同号,且a、b的符号与p的符号相同;
当q<0时,a、b异号,且绝对值较大的因数与p的符号相同。
掌握一定的规律去找a、b,可以减少尝试的次数。
说明:先把二次项系数为1的做熟、掌握技巧方法。请你认真完成附件中的练习。
⑥二次项系数不是1的二次三项式ax^2+bx+c(a≠0),它的方法是“拆两头,凑中间”,这里要确定4个常数,分析和尝试都要比二次项系数为1的情况复杂,建议用画十字图的办法确定。
说明:二次项系数不是1的二次三项式十字相乘法、非二次三项式的多项式因式分解是难点。会在后一节中跟进练习。
4.练习
见附件“因式分解-十字相乘法”.